Sistemas y Mecanismos encontrados en nuestro dia a dia

Sistema de Levas

Utilidad

Permite obtener un movimiento lineal alternativo, o uno oscilante, a partir de uno giratorio; pero no nos permite obtener el giratorio a partir de uno lineal alternativo (o de uno oscilante). Es un mecanismo no reversible.

Este mecanismo se emplea en: motores de automóviles (para la apertura y cierre de las válvulas), programadores de lavadoras (para la apertura y cierre de los circuitos que gobiernan su funcionamiento), carretes de pesca (mecanismo de avance-retroceso del carrete), cortapelos, depiladoras, cerraduras.

Descripción

Para su correcto funcionamiento, este mecanismo necesita, al menos: árbol, soporte, leva y seguidor de leva (palpador) acompañado de un sistema de recuperación (muelle, resorte...).

• El árbol es el eje de giro de la leva y el encargado de transmitirle su movimiento giratorio.
• El soporte es el encargado de mantener unido todo el conjunto y, normalmente, guiar el movimiento del seguidor
• La leva es siempre la que recibe el movimiento giratorio a través del eje o del árbol en el que está montada. Su perfil hace que el seguidor ejecute un ciclo de movimientos muy preciso.
• El seguidor (palpador) apoya directamente sobre el perfil de la leva y se mueve a medida que ella gira. Para conseguir que el seguidor esté permanentemente en contacto con la leva es necesario dotarlo de un sistema de recuperación (normalmente un muelle o un resorte)

La leva va solidaria con un eje (árbol) que le transmite el movimiento giratorio; en muchas aplicaciones se recurre a montar varias levas sobre un mismo eje o árbol (árbol de levas), lo que permite la sincronización del movimiento de varios seguidores a la vez.

Seguidor de leva

Según el tipo de movimiento que queramos obtener a la salida, se puede recurrir a dos tipos de seguidores: émbolo y palanca

Émbolo, si queremos que el movimiento de salida sea lineal alternativo.

En el ejemplo vemos el sistema simplificado de distribución del motor de un coche. La válvula actúa como émbolo y se combina con un empujador, que es el que está en contacto directo con la leva gracias a al acción del muelle.

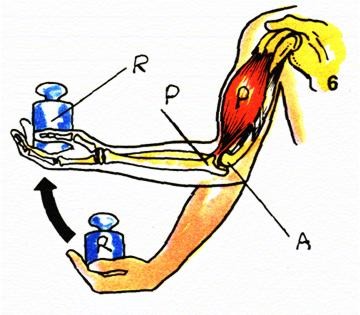
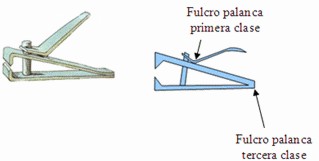
Palanca, si queremos que el movimiento de salida sea oscilante.

En este caso emplearemos la palanca de primer o tercer grado para amplificar el movimiento y la de primero o segundo para atenuarlo.

El mecanismo suele complementarse con un muelle de recuperación que permite que el palpador (seguidor de leva) se mantenga en contacto con el perfil de la biela en todo momento.

Características

En los mecanismos de levas, el diseño del perfil de leva siempre estará en función del movimiento que queramos que realice el seguidor de leva. Dicho de otro modo: la leva es el resultado del movimiento que deseemos obtener en el seguidor, por tanto, antes de construir la leva tenemos que saber cuál es el movimiento que queremos obtener.

Excéntrica-Biela-Palanca

Utilidad

Permite obtener un movimiento giratorio continuo a partir de uno oscilante, o también, obtener un movimiento oscilante a partir de uno giratorio continuo.

Se puede encontrar en las máquinas de coser (para obtener el movimiento giratorio necesario en la máquina a partir del oscilante del pie), en los limpiaparabrisas de los automóviles

Descripción

Este mecanismo emplea, al menos, una excéntrica (o una manivela ), una biela y una palanca colocados sobre un soporte único y conectados de la forma siguiente:

Desde el punto de vista de la palanca se nos pueden presentar dos casos:

· Cuando transformamos giratorio en oscilante, la potencia es suministrada por la biela a la palanca (el pie de biela será el punto de aplicación de la potencia).

· Cuando transformamos oscilante en giratorio, el mecanismo biela-manivela es la resistencia y el pie de biela es el punto de aplicación de la resistencia.

Características

Elección de la palanca adecuada.

La palanca puede ser de cualquier orden (1º, 2º ó 3º) y su elección estará en función de la utilidad que le queramos dar a la máquina.

· Cuando la máquina produce movimiento giratorio a partir de uno oscilante es frecuente emplear una palanca de tercer grado, así el movimiento de la potencia (normalmente el pie) es pequeño en relación al de la resistencia (pie de biela) y se pueden alcanzar mayores velocidades de giro.

• Cuando se emplea para producir un movimiento oscilante a partir de uno giratorio, la elección de la palanca dependerá de factores tales como sentido del movimiento, fuerza que tiene que crear y amplitud de la oscilación (ver el apartado referido a palancas para analizar cuál sería la elección más adecuada)

Un poco de historia.

El empleo de la manivela (eje acodado que se accionaba con las manos) para obtener un movimiento giratorio continuo en pequeñas máquinas tenía el inconveniente de dejar una sola mano libre para realizar el trabajo (hacer hilos, afilar, coser...), por lo que fue necesario inventar un sistema que liberase esa mano y permitiera emplear las dos de forma útil.

La solución llegó hacia 1530 cuando apareció la rueca de pedal (Johan Jürgens), lo que permitió mantener libres las dos manos para atender la fabricación de los hilos (más adelante este mismo sistema se aplicó a piedras de afilar y mucho más tarde a máquinas de coser). La rueca de pedal introdujo el sistema palanca-biela-excéntrica que sustituyó a sistemas anteriores, siendo posiblemente la primera aplicación práctica del sistema biela-manivela.

Cigüeñal-Biela

Utilidad

Permite conseguir que varias bielas se muevan de forma sincronizada con movimiento lineal alternativo a partir del giratorio que se imprime al eje del cigüeñal, o viceversa.

Este mecanismo se emplea para la sincronización de acciones a partir de un movimiento giratorio; se puede encontrar en el accionamiento secuencial de interruptores, juguetes, limpiaparabrisas...

Añadiéndole un émbolo forma el mecanismo básico de los motores de combustión interna, permitiendo producir un movimiento giratorio a partir del alternativo de varios pistones cuyos puntos muertos no se producen al mismo tiempo.

Descripción

Este mecanismo emplea un cigüeñal sobre cuyas muñequillas se han conectado sendas bielas, lo que permite obtener un comportamiento, por cada biela, similar al sistema biela-manivela.

El sistema suele complementarse con un émbolo para guiar mejor el movimiento alternativo del pie de biela. En los motores de combustión interna el propio émbolo hace de pistón.

La longitud de los brazos de las diferentes manivelas que componen el cigüeñal determina la carrera, mientras que su posición determina lasecuencia.

Características

A la hora de diseñar estos mecanismos tenemos que tener en cuenta que:

• Para que el sistema funcione correctamente se deben emplear bielas cuya longitud sea, al menos, 4 veces el radio de giro de la manivela a la que está acoplada.
• Como el mecanismo está formado por varias manivelas acopladas en serie, es necesario que los cuellos del cigüeñal (partes de eje que quedan entre las manivelas) descansen sobre soportes adecuados, esto evita que el cigüeñal entre en flexión y deje de funcionar correctamente.
• Las cabezas de las bielas deben de estar centradas en la muñequilla sobre la que giran, por lo que puede ser necesario aumentar su anchura (colocación de un casquillo).

Mecanismos Diferenciales

Mecanismo diferencial

Un diferencial es el elemento mecánico que permite que las ruedas derecha e izquierda de un vehículo giren a revoluciones diferentes, según éste se encuentre tomando una curva hacia un lado o hacia el otro.

Cuando un vehículo toma una curva, por ejemplo hacia la derecha, la rueda derecha recorre un camino más corto que la rueda izquierda, ya que esta última se encuentra en la parte exterior de la curva.

Antiguamente, las ruedas de los vehículos estaban montadas de forma fija sobre un eje. Este hecho significaba que una de las dos ruedas no giraba bien, desestabilizando el vehículo. Mediante el diferencial se consigue que cada rueda pueda girar correctamente en una curva, sin perder por ello la fijación de ambas sobre el eje, de manera que la tracción del motor actúa con la misma fuerza sobre cada una de las dos ruedas.

El diferencial consta de engranajes dispuestos en forma de "U" en el eje. Cuando ambas ruedas recorren el mismo camino, por ir el vehículo en línea recta, el engranaje se mantiene en situación neutra. Sin embargo, en una curva los engranajes se desplazan ligeramente, compensando con ello las diferentes velocidades de giro de las ruedas.

La diferencia de giro también se produce entre los dos ejes. Las ruedas directrices describen una circunferencia de radio mayor que las no directrices, por ello se utiliza el diferencial.

Un vehículo con tracción en las cuatro ruedas puede tener hasta tres diferenciales: uno en el eje frontal, uno en el eje trasero y un diferencial central.

En el hipotético caso de que ambos ejes sean directrices, el que tenga mayor ángulo de giro describirá un radio mayor.

Funcionamiento de los Engranajes Planetarios

Los engranajes planetarios están compuestos por tres miembros: Piñón planetario, el Portasatélites y la Corona.

Ventajas:
• Son compactos
• Los planetarios siempre van engranados constante y completamente, eliminando la posibilidad de que se produzcan daños en los dientes debido a choques en las maniobras de engrane.
• Son fuertes y robustos, pudiendo soportar cargas de par mayores en comparación con otras combinaciones de engranajes de transmisiones manuales.

Su funcionamiento esta gobernado por cinco estados que proporcionan la clave para entender los diferentes flujos de potencia de engranajes en las transmisiones automáticas. Pasemos a ver estos estados.

Estado Neutro: Ninguno de los elementos del planetario esta bloqueado. (Punto muerto). En la figura 1 el piñón actúa como miembro de entrada conductor, y los satélites rotan libremente sobres sus ejes pues la corona también puede girar libremente.

Estado de Reducción: (Reducción de Marcha) Pongamos un elemento de reacción (fijo) como ser la corona y que la salida sea el portasatélite el cual transmitirá el movimiento a las ruedas. Ver figura 2.

En este caso el par es multiplicado y la velocidad se reduce de acuerdo con el factor de relación de transmisión. Ej. Una relación de 3 : 1 cambia un par de entrada de 100 [Nm] y una velocidad de entrada de 2.700 [rpm] en un par de salida de 300 [Nm] y 900 [rpm]

Estado de Supermarcha: cuando tenemos un elemento de reacción (fijo) y el portasatélites es la entrada, en este caso tenemos una multiplicación del giro, produciendo un efecto contrario al Estado de Reducción de Marcha, reduciendo el par y aumentando la velocidad.
En la figura 3a y 3b podemos ilustrar esto. Fig. 3a con el piñón planetario estacionarios, vemos el sentido de giro del portasatélites y el arrastre de la corona.

Estado de transmisión directa: Obtenemos este estado bloqueando entre sí dos miembros cualesquiera del tren de engranajes planetarios. Conducir dos miembros al mismo tiempo con relación a la velocidad y en la misma dirección produce el mismo efecto.

Estado de Inversa: Este estado lo obtenemos reteniendo el portasatélite para que no rote, entonces la corona y el piñón tendrán sentido de giro distintos, sea que la entrada fuere por el piñón y la salida por la corona o viceversa.

Sistema de engranajes.

Prácticamente las mayorías de las cajas automáticas utilizan dos sistemas de engranajes o derivaciones de estas. Estos son el sistema Simpson y el Sistema Ravigneaux.

Sistema Simpson: consisten en dos trenes de planetarios que comparten los planetarios y un árbol de salida. Esta integración de los planetarios comunes ofrece una clasificación adicional del conjunto denominándolo también planetario compuesto.

Sistema Ravigneaux: Sus característica es poseer tres conjuntos de satélites dobles, cada conjunto de satélites esta compuesto por un piñón corto y otro largo y dos engranajes planetarios independientes que se engranan con los satélites doble del portasatélites.
Como ejercicio a continuación se presentan los dos sistemas para ser analizado.

Mecanismos (cortesia de tutv.com)

L famoso autor de la celebre frase "Dadme un punto de apoyo y moveré el mundo"

Arquimedes

(Siracusa, actual Italia, h. 287 a.C.-id., 212 a.C.) Matemático griego. Hijo de un astrónomo, quien probablemente le introdujo en las matemáticas, Arquímedes estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes; a este último dedicó Arquímedes su Método, en el que expuso su genial aplicación de la mecánica a la geometría, en la que «pesaba» imaginariamente áreas y volúmenes desconocidos para determinar su valor. Regresó luego a Siracusa, donde se dedicó de lleno al trabajo científico.

De la biografía de Arquímedes, gran matemático e ingeniero, a quien Plutarco atribuyó una «inteligencia sobrehumana», sólo se conocen una serie de anécdotas. La más divulgada la relata Vitruvio y se refiere al método que utilizó para comprobar si existió fraude en la confección de una corona de oro encargada por Hierón II, tirano de Siracusa y protector de Arquímedes, quizás incluso pariente suyo. Hallándose en un establecimiento de baños, advirtió que el agua desbordaba de la bañera a medida que se iba introduciendo en ella; esta observación le inspiró la idea que le permitió resolver la cuestión que le planteó el tirano. Se cuenta que, impulsado por la alegría, corrió desnudo por las calles de Siracusa hacia su casa gritando «Eureka! Eureka!», es decir, «¡Lo encontré! ¡Lo encontré!».

La idea de Arquímedes está reflejada en una de las proposiciones iniciales de su obra Sobre los cuerpos flotantes, pionera de la hidrostática; corresponde al famoso principio que lleva su nombre y, como allí se explica, haciendo uso de él es posible calcular la ley de una aleación, lo cual le permitió descubrir que el orfebre había cometido fraude.

Según otra anécdota famosa, recogida por Plutarco, entre otros, Arquímedes aseguró al tirano que, si le daban un punto de apoyo, conseguiría mover la Tierra; se cree que, exhortado por el rey a que pusiera en práctica su aseveración, logró sin esfuerzo aparente, mediante un complicado sistema de poleas, poner en movimiento un navío de tres mástiles con su carga.

Son célebres los ingenios bélicos cuya paternidad le atribuye la tradición y que, según se dice, permitieron a Siracusa resistir tres años el asedio romano, antes de caer en manos de las tropas de Marcelo; también se cuenta que, contraviniendo órdenes expresas del general romano, un soldado mató a Arquímedes por resistirse éste a abandonar la resolución de un problema matemático en el que estaba inmerso, escena perpetuada en un mosaico hallado en Herculano.

Esta pasión de Arquímedes por la erudición, que le causó la muerte, fue también la que, en vida, se dice que hizo que hasta se olvidara de comer y que soliera entretenerse trazando dibujos geométricos en las cenizas del hogar o incluso, al ungirse, en los aceites que cubrían su piel. Esta imagen contrasta con la del inventor de máquinas de guerra del que hablan Polibio y Tito Livio; pero, como señala Plutarco, su interés por esa maquinaria estribó únicamente en el hecho de que planteó su diseño como mero entretenimiento intelectual.

El esfuerzo de Arquímedes por convertir la estática en un cuerpo doctrinal riguroso es comparable al realizado por Euclides con el mismo propósito respecto a la geometría; esfuerzo que se refleja de modo especial en dos de sus libros: en los Equilibrios planos fundamentó la ley de la palanca, deduciéndola a partir de un número reducido de postulados, y determinó el centro de gravedad de paralelogramos, triángulos, trapecios, y el de un segmento de parábola. En la obra Sobre la esfera y el cilindro utilizó el método denominado de exhaustión, precedente del cálculo integral, para determinar la superficie de una esfera y para establecer la relación entre una esfera y el cilindro circunscrito en ella. Este último resultado pasó por ser su teorema favorito, que por expreso deseo suyo se grabó sobre su tumba, hecho gracias al cual Cicerón pudo recuperar la figura de Arquímedes cuando ésta había sido ya olvidada.

Palancas

El hombre, desde los inicios de los tiempos ha ideado mecanismos que le permitan ahorrar energía y con ello lograr que sus esfuerzos físicos sea cada vez menores.

Entre los diversos mecanismos para hacer más eficientes sus esfuerzos se pueden citar las poleas, los engranajes y las palancas.

La palanca es una máquina simple que se emplea en una gran variedad de aplicaciones.

Probablemente, incluso, las palancas sean uno de los primeros mecanismos ingeniados para multiplicar fuerzas. Es cosa de imaginarse el colocar una gran roca como puerta a una caverna o al revés, sacar grandes rocas para habilitar una caverna.

Con una buena palanca es posible mover los más grandes pesos y también aquellos que por ser tan pequeños también representan dificultad para tratarlos.

Se cuenta que el propio Galileo Galilei habría dicho: "Dadme un punto de apoyo y moveré el mundo". En realidad, obtenido ese punto de apoyo y usando una palanca suficientemente larga, eso es posible.

En nuestro diario vivir son muchas las veces que “estamos haciendo palanca”. Desde mover un dedo o un brazo o un pie hasta tomar la cuchara para beber la sopa involucra el hacer palanca de una u otra forma.

Ni hablar de cosas más evidentes como jugar al balancín, hacer funcionar una balanza, usar un cortaúñas, una tijera, un diablito (sacaclavos), etc.

Casi siempre que se pregunta respecto a la utilidad de una palanca, la respuesta va por el lado de que “sirve para multiplicar una fuerza”, y eso es cierto pero prevalece el sentido que multiplicar es aumentar, y no es así siempre, a veces el multiplicar es disminuir (piénsese en multiplicar por un número decimal, por ejemplo).

¿Qué es una palanca?

Básicamente está constituida por una barra rígida, un punto de apoyo (se le puede llamar “fulcro”) y dos fuerzas (mínimo) presentes: una fuerza (o resistencia) a la que hay que vencer (normalmente es un peso a sostener o a levantar o a mover en general) y la fuerza (o potencia) que se aplica para realizar la acción que se menciona. La distancia que hay entre el punto de apoyo y el lugar donde está aplicada cada fuerza, en la barra rígida, se denomina brazo. Así, a cada fuerza le corresponde un cierto brazo.

Como en casi todos los casos de máquinas simples, con la palanca se trata de vencer una resistencia, situada en un extremo de la barra, aplicando una fuerza de valor más pequeño que se denomina potencia, en el otro extremo de la barra.

En una palanca podemos distinguir entonces los siguientes elementos:

El punto de apoyo o fulcro.

Potencia: la fuerza (en la figura de abajo: esfuerzo) que se ha de aplicar.

Resistencia: el peso (en la figura de abajo: carga) que se ha de mover.

El brazo de potencia (b₂) : es la distancia entre el fulcro y el punto de la barra donde se aplica la potencia.

El brazo de resistencia (b₁): es la distancia entre el fulcro y el punto de la barra donde se encuentra la resistencia o carga.

¿Cuántos tipos de palanca hay?

Según lo visto en la figura y lo definido en el cuadro superior, hay tres tipos de palancas:

Palanca de primer tipo o primera clase o primer grupo o primer género:

Se caracteriza por tener el fulcro entre la fuerza a vencer y la fuerza a aplicar.

Esta palanca amplifica la fuerza que se aplica; es decir, consigue fuerzas más grandes a partir de otras más pequeñas.

Por ello, con este tipo de palancas pueden moverse grandes pesos, basta que el brazo b1 sea más pequeño que el brazo b2.

Algunos ejemplos de este tipo de palanca son: el alicates, la balanza, la tijera, las tenazas y el balancín.

Algo que desde ya debe destacarse es que al accionar una palanca se producirá un movimiento rotatorio respecto al fulcro, que en ese caso sería el eje de rotación.

Palanca de segundo tipo o segunda clase o segundo grupo o segundo género:

Se caracteriza porque la fuerza a vencer se encuentra entre el fulcro y la fuerza a aplicar.

Este tipo de palanca también es bastante común, se tiene en lo siguientes casos: carretilla, destapador de botellas, rompenueces.

También se observa, como en el caso anterior, que el uso de esta palanca involucra un movimiento rotatorio respecto al fulcro que nuevamente pasa a llamarse eje de rotación.

Palanca de tercer tipo o tercera clase o tercer grupo:

Se caracteriza por ejercerse la fuerza “a aplicar” entre el fulcro y la fuerza a vencer.

Este tipo de palanca parece difícil de encontrar como ejemplo concreto, sin embargo… el brazo humano es un buen ejemplo de este caso, y cualquier articulación es de este tipo, también otro ejemplo lo tenemos al levantar una cuchara con sopa o el tenedor con los tallarines, una corchetera funciona también aplicando una palanca de este tipo.

Este tipo de palanca es ideal para situaciones de precisión, donde la fuerza aplicada suele ser mayor que la fuerza a vencer.

Y, nuevamente, su uso involucra un movimiento rotatorio.

Hemos visto los tres tipos de palancas, unos se usan más que otros, pero los empleamos muy a menudo, a veces sin siquiera darnos cuenta, y sin pensar en el tipo de palanca que son cuando queremos aplicar su funcionamiento en algo específico.

En algunas ocasiones, ciertos artefactos usan palancas de más de un tipo en su funcionamiento, son las palancas múltiples.

Palancas múltiples: Varias palancas combinadas.

Por ejemplo: el cortaúñas es una combinación de dos palancas, el mango es una combinación de 2º género que presiona las hojas de corte hasta unirlas. Las hojas de corte no son otra cosa que las bocas o extremos de una pinza y, constituyen, por tanto, una palanca de tercer género.

Otro tipo de palancas múltiples se tiene en el caso de una máquina retroexcavadora, que tiene movimientos giratorios (un tipo de palanca), de ascenso y descenso (otra palanca) y de avanzar o retroceder (otra palanca).

Ley de las palancas

Desde el punto de vista matemático hay una ley muy importante, que antiguamente era conocida como la “ley de oro”, nos referimos a la Ley de las Palancas:

El producto de la potencia por su brazo (F2 • b2) es igual al producto de la resistencia por el brazo suyo (F1 • b1)

lo cual se escribe así:

F1 • b1 = F2 • b2

lo que significa que:

Trabajo motor = Trabajo resistente

Llamando F1 a la fuerza a vencer y F2 a la fuerza a aplicar y recordando que b1 es la distancia entre el fulcro y la fuerza a vencer y b2 la distancia entre el fulcro y el lugar donde se ha de aplicar la fuerza F2. En este caso se está considerando que las fuerzas son perpendiculares a los brazos.

Y es válida para todo tipo de palancas.

Ahora bien, ¿en qué se sostiene la Ley de las Palancas?

En un concepto mucho más amplio, el concepto de “torque”.

Al comentar las características de cada tipo de palanca, dijimos que su uso involucra siempre un movimiento rotatorio. Bien, cada vez que se realiza, o se intenta realizar, un movimiento rotatorio se realiza lo que se denomina “torque”.

Torque es la acción que se realiza mediante la aplicación de una fuerza a un objeto que debido a esa fuerza adquiere o puede adquirir un movimiento rotatorio.

Abrir una puerta involucra la realización de torque. El eje de rotación son las bisagras.

Abrir un cuaderno involucra la realización de torque. El eje de rotación es el lomo o el espiral.

Jugar al balancín es hacer torque. El eje de rotación es el punto de apoyo.

Al mover un brazo se realiza torque. El eje de rotación es el codo.

Dos situaciones excepcionales hay que distinguir:

- Cuando se aplica la fuerza en el eje de rotación no se produce rotación, en consecuencia no hay torque. ¿Se imaginan ejercer una fuerza en una bisagra para abrir una puerta?

- Cuando se aplica la fuerza en la misma dirección del brazo tampoco se realiza rotación, por lo tanto tampoco hay torque. O, mejor dicho, el torque es nulo. Imagínense atar una cuerda al borde de la tapa de un libro y tirar de él, paralelo al plano del libro, tratando de abrirlo.

Ya que mencionamos el caso de situaciones particulares donde el torque que se realiza resulta ser nulo, destaquemos también que el torque es máximo cuando el ángulo entre el brazo y la fuerza a aplicar es un ángulo recto (90º y 270º). Otros casos, donde el ángulo entre la fuerza aplicada y el brazo no es ni recto ni nulo ni extendido (0º o 180º) necesitan de matemática que en estos momentos no están al alcance.

El lector más avanzado puede trabajar con el concepto, matemático, de torque como igual al producto entre la fuerza aplicada, la longitud del brazo y el seno del ángulo que forman la fuerza aplicada y el brazo.